Keplerの法則
Keplerの法則
惑星の運動に関して、以下の3つの法則が成り立つことが分かっている(Keplerの法則)。
第一法則(楕円軌道の法則)
太陽系の惑星は太陽を焦点とする楕円軌道上を動く。
第二法則(面積速度一定の法則)
単位時間に惑星と太陽間の動径が掃く面積(面積速度)は一定である。
第三法則(調和の法則)
惑星の公転周期の2乗は、軌道長半径の3乗に比例する。
以下では、これらの法則の証明をしていこうと思う。
第二法則(面積速度一定の法則)
Kepler問題では、$ \ \boldsymbol{F} \parallel \boldsymbol{r} \ $のような中心力が働いている場合を考える。このとき運動方程式の章より、角運動量は保存する。したがって、
\begin{eqnarray}
\dot{L}
&=&\frac{d}{dt}(mrv_\perp)\\
&=&\frac{d}{dt}(mr_\perp v)\\
&=&0\tag{1}
\end{eqnarray}
が成り立つ。また、面積速度に関しては以下の図より、
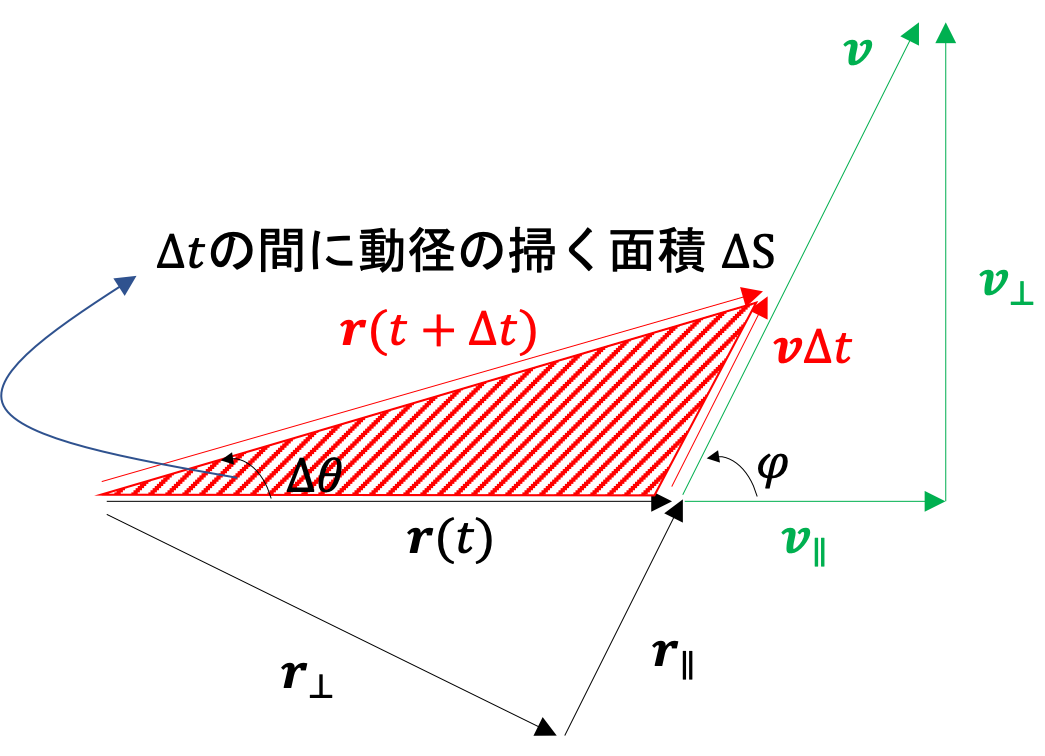
\begin{eqnarray}
\Delta S
&=&\frac{1}{2}rv\Delta t\sin \varphi\\
&=&\frac{1}{2}rv_\perp\Delta t\\
&=&\frac{1}{2}r_\perp v\Delta t\tag{2}
\end{eqnarray}]
となる。(1)、(2)より、面積速度$ \ \dot{S}=\frac{dS}{dt}\ $は、
\[\dot{S}=\frac{1}{2}r_\perp v=\frac{L}{2m}\tag{3}\]
となり保存することがわかる。
また、面積速度は、$ \ \theta \ $を用いて表せば、
\begin{eqnarray}
\Delta S
&=&\frac{1}{2}r(t)r(t+\Delta t)\sin \Delta \theta\\
\end{eqnarray}
より、
\[\dot{S}=\frac{1}{2}r^2\dot{\theta}\tag{4}\]
とも書ける。
第一法則(楕円軌道の法則)
太陽の質量を$ \ M \ $、惑星の質量を$ \ m \ $とすると、力学的エネルギー$ \ E \ $は
\[E=\frac{1}{2}m(v_\perp ^2+v_\parallel ^2)-\frac{GMm}{r}\tag{5}\]
と書ける。これは(2)、(3)より$ \ v_\perp = \frac{L}{mr} \ $であり、また、$ \ v_\parallel=\dot{r}\ $であるから、
\[E=\frac{1}{2}m\dot{r}^2+m(\frac{L^2}{2m^2r^2}-\frac{GM}{r})\tag{6}\]
とも書ける。ここで(6)式の第二項はどちらも$ \ r \ $のみに依存する項であるから、まとめて一つのポテンシャルのように捉えることができ、有効ポテンシャル$ \ U_{eff}\ $と呼ぶ。ここで(3)、(4)より、
\[d\theta=\frac{L}{mr^2}dt\tag{7}\]
また(6)式を変形して、
\[dt=\pm\frac{dr}{\sqrt{\frac{2}{m}(E-m(\frac{L^2}{2m^2r^2}-\frac{GM}{r}))}}\tag{8}\]
(7)、(8)を用いて積分を実行し、変形していくと以下のようになる。
\begin{eqnarray}
\theta
&=&\pm\int\frac{Ldr}{r^2\sqrt{2m(E-m(\frac{L^2}{2m^2r^2}-\frac{GM}{r}))}}+const.\\
&=&\pm\int\frac{Ldr}{r\sqrt{2mEr^2-L^2+2GMm^2r}}+const.\\
\end{eqnarray}
$ \ z = \frac{1}{r} \ $と置換し整理すると、
\begin{eqnarray}
\theta
&=&\mp\int\frac{dz}{\sqrt{\frac{2mE}{L^2}-z^2+\frac{2GMm^2}{L^2}z}}+const.\\
&=&\mp\int\frac{dz}{\sqrt{\frac{2mE}{L^2}+\frac{G^2M^2m^4}{L^4}-(z-\frac{GMm^2}{L^2})^2}}+const.\\
\end{eqnarray}
ここで、$ \ (\arccos x)' = -\frac{1}{\sqrt{1-x^2}} \ $を用いると、積分定数を$ \ \alpha \ $として
\[\pm\arccos \frac{z-\frac{GMm^2}{L^2}}{\sqrt{\frac{2mE}{L^2}+\frac{G^2M^2m^4}{L^4}}}=\theta-\alpha\]
\[\therefore \cos(\theta-\alpha)= \frac{\frac{1}{r}-\frac{GMm^2}{L^2}}{\sqrt{\frac{2mE}{L^2}+\frac{G^2M^2m^4}{L^4}}}\]
\[\therefore r = \frac{\frac{L^2}{GMm^2}}{1+\sqrt{1+\frac{2EL^2}{G^2M^2m^3}}\cos (\theta-\alpha)}\]
$ \ l = \frac{L^2}{GMm^2}, e=\sqrt{1+\frac{2EL^2}{G^2M^2m^3}} \ $とおくと、
\[r = \frac{l}{1+e\cos (\theta-\alpha)}\tag{9}\]
と書ける。これは$ \ l \ $を半直弦、$ \ e \ $を離心率とする二次曲線の極座標表示と一致する。惑星の運動は有界であるから、楕円運動をしていることが導かれる。
軌道と力学的エネルギー
$ \ e=\sqrt{1+\frac{2EL^2}{G^2M^2m^3}} \ $であり、二次曲線は$ \ 0\lt e\lt 1 \ $:楕円、$ \ e\gt 1 \ $:双曲線となるから、力学的エネルギー$ \ E \ $の符号により軌道の形状が決まる。
力学的エネルギー$ \ E \ $は無限遠方での運動エネルギーを表しているのであったから、それが負である場合は太陽系内に拘束されており、楕円軌道を描く。逆に正であった場合は、その天体は太陽系外部の天体であり、双曲線軌道を描くことになる。
第三法則(調和の法則)
ここまでくれば第三法則は楕円の式を用いるだけである。(周期) = (楕円の面積)/(面積速度)であるから、周期、長軸半径、短軸半径をそれぞれ$ \ T,a,b \ $と表記すると、
\begin{eqnarray}
T
&=& \frac{\pi ab}{\frac{L}{2m}}\\
&=& 2m\frac{\pi a\sqrt{al}}{\sqrt{GMm^2l}}\\
&=& 2\pi\frac{a^{\frac{3}{2}}}{\sqrt{GM}}
\end{eqnarray}
\[\therefore \frac{T^2}{a^3}=\frac{4\pi^2}{GM}=const.\tag{10}\]
以上より、第三法則は成り立つことが分かる。
