多粒子系の運動
外力と内力
$ \ N(\geq 3) \ $粒子からなる多粒子系では、一粒子系の場合と異なり、多粒子系の中の各粒子に働く力は、系外からの力及び慣性力、つまり外力(external force)と、系内の他の粒子から働く力、つまり内力(または相互作用、interaction)に分別される。ここでは、多粒子系の中の$i$番目の粒子の質量を$ \ m_i \ $、位置ベクトルを$ \ \boldsymbol{r}_i(i=1,2,\cdots,N) \ $、 $i$番目の粒子に働く外力を$ \ \boldsymbol{F}^{(ex)}_i(i=1,2,\cdots,N) \ $、また、$i$番目の粒子に$j$番目$(j\neq i)$の粒子から働く内力を$ \ \boldsymbol{F}^{(in)}_{ij}(i=1,2,\cdots,N) \ $(もしくは単に、$ \ \boldsymbol{F}_{ij}(i=1,2,\cdots,N) \ $)と表記する。
多粒子系の重心運動と内部運動
$i$番目$(i=1,2,\cdots,N)$の粒子の運動について、運動方程式は以下のようになる。
$m_i\ddot{\boldsymbol{r}}_i=\dot{\boldsymbol{p}_i}=\boldsymbol{F}^{(ex)}_i+\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}\tag{1}$
$ \ N\geq 3 \ $では、この複雑な連立微分方程式の厳密な解は存在せず、特殊な場合を除いて解くことはできない。一方$ \ N\leq 2 \ $では解析可能で、次章で詳しく解説しようと思う。この章では、$ \ N\geq 3 \ $の場合でも、重心(center of gravity)、または質量中心(center of mass)を定義することで、複雑な粒子系の運動でも特徴を把握できることを示そう。
ここで、Newtonの運動の三法則のうちの第三法則(作用・反作用の法則)を思い出そう。それは以下のような法則であった。
第三法則(作用・反作用の法則)…
二つの質点1,2の間に相互に力が働くとき、質点1から質点2に作用する力$ \ \boldsymbol{F}_{12} \ $と、質点2から質点1に作用する力$ \ \boldsymbol{F}_{21} \ $は、大きさが等しく逆向きで、$ \ \boldsymbol{F}_{12}=-\boldsymbol{F}_{21} \ $が成り立つ。
これを利用して(1)の式を$i=1,2,\cdots,N$について足すと、例えば$ \ \boldsymbol{F}_{12}+\boldsymbol{F}_{21}=\boldsymbol{0} \ $のようになり、それぞれの質点に働く内力が相殺するから以下の式を得る。
$\displaystyle\sum_{i}m_i\ddot{\boldsymbol{r}}_i=\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_i\tag{2}$
ここで、多粒子系の全質量を
$M=\displaystyle\sum_{i}m_i\tag{3}$
多粒子系の重心の位置ベクトルを
$\boldsymbol{r}_G=\displaystyle\frac{\displaystyle\sum_{i}m_i\boldsymbol{r}_i}{M}\tag{4}$
と定義すると、(2)は以下のように変形される。
$M\ddot{\boldsymbol{r}}_G=\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_i\tag{5}$
この式は重心運動方程式と呼ばれ、この式からは多粒子系の重心の運動の特徴を読み取ることができる。それは、各粒子が内力によって相対位置が時間的に変化していたとしても、多粒子系の重心の運動はは外力のみに依存し、内力に依らず、また、重心の運動は、重心の位置に多粒子系の全質量が集中しておりその点に全外力が働いたと考える場合と同じ運動をするということである。
以下では、多粒子系の運動を、代表点と考えられる重心の運動(重心運動)と重心から見た各粒子の運動(内部運動)に分けて、運動方程式をいじくりまわすことで複雑な粒子系の特徴を探っていこう。
運動量
多粒子系の全運動量$ \ \boldsymbol{P} \ $について以下が成り立つ。
\begin{eqnarray}
\boldsymbol{P}=\displaystyle\sum_{i}\boldsymbol{p}_i&=&M\displaystyle\frac{\displaystyle\sum_{i}m_i\dot{\boldsymbol{r}}_i}{M}\\&=&M\boldsymbol{v}_G\\&=&\boldsymbol{P}_G\tag{6}
\end{eqnarray}
ここで、$ \ \boldsymbol{P}_G=M\boldsymbol{v}_G \ $は、重心運動量と呼ばれ、重心の位置に全質量が集中したと考える場合の重心の運動量を表す。一方(3)、(4)より、
\[\boldsymbol{r}_G=\displaystyle\frac{\displaystyle\sum_{i}m_i\boldsymbol{r}_i}{\displaystyle\sum_{i}m_i}\]
$\therefore\displaystyle\sum_{i}m_i(\boldsymbol{r}_i-\boldsymbol{r}_G)=\displaystyle\sum_{i}m_i\boldsymbol{r}_{iG}=\boldsymbol{0}\tag{7}$
ここで、重心から見た各粒子の位置ベクトルを以下のように表記した。(速度ベクトル、加速度ベクトルについても同様に表記)
$\boldsymbol{r}_{iG}=\boldsymbol{r}_i-\boldsymbol{r}_G\tag{8}$
よって、重心から見た各粒子の運動量の合計$ \ \boldsymbol{P}_{in}=\displaystyle\sum_{i}m_i\dot{\boldsymbol{r}}_{iG}=\displaystyle\sum_{i}m_i\boldsymbol{v}_{iG} \ $については、(7)より、
$\boldsymbol{P}_{in}=\frac{d}{dt}(\displaystyle\sum_{i}m_i\boldsymbol{r}_{iG})=\boldsymbol{0}\tag{9}$
が成り立つ。これは、重心から見た各粒子の運動量の合計は必ず$ \ \boldsymbol{0} \ $になるということをである。
以上(5)、(6)、(9)より結論をまとめると、
\begin{eqnarray}
\left\{ \begin{array}{l}
\boldsymbol{P}=\boldsymbol{P}_G, \ \boldsymbol{P}_{in}=\boldsymbol{0}\\
\\
\dot{\boldsymbol{P}}=\dot{\boldsymbol{P}}_G=\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_i\\
\end{array} \right.\tag{10} \end{eqnarray}
この結果より、$ \ \displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_i=\boldsymbol{0} \ $なら、$ \ \boldsymbol{P}= \ $一定で、このとき、$ \ \boldsymbol{v}_G= \ $一定なので、重心速度は一定であることがわかる。すなわち、外力が働かない系では系全体の運動量は保存し、それはすなわち重心速度が保存することと同義であることがわかる。また、成分に分解してもこれは成り立つ。$ \ \boldsymbol{F}=\dot{\boldsymbol{P}} \ $であることより、ベクトル$ \ \boldsymbol{A} \ $の$i$成分$(i=x,y,z)$を$ \ \boldsymbol{A}_i \ $と表記すると、特に、外力の$x$成分がないとき、つまり$ \ (\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_i)_x=\boldsymbol{0} \ $なら、$ \ \boldsymbol{P}_x= \ $一定で、このとき、$ \ \boldsymbol{v}_{Gx}= \ $一定なので、重心速度の$x$成分は一定であるということである。
運動エネルギー
多粒子系の全運動エネルギー$ \ K \ $について以下が成り立つ。($\because(9)$)
\begin{eqnarray}
K
&=&\displaystyle\sum_{i}K_i\\
&=&\displaystyle\sum_{i}\frac{1}{2}m_iv_i^2\\
&=&\displaystyle\sum_{i}\frac{1}{2}m_i|\boldsymbol{v}_G+\boldsymbol{v}_{iG}|^2\\
&=&\frac{1}{2}(\displaystyle\sum_{i}m_i)v_G^2\\
&+&\displaystyle\sum_{i}\frac{1}{2}m_iv_{iG}^2\\
&+&\boldsymbol{v}_G\cdot\displaystyle\sum_{i}m_i\boldsymbol{v}_{iG}\\
&=&\frac{1}{2}Mv_G^2+\displaystyle\sum_{i}\frac{1}{2}m_iv_{iG}^2\tag{11}
\end{eqnarray}
(11)の第一項を重心運動エネルギー$ \ K_G \ $、第二項を内部運動エネルギー$ \ K_{in} \ $と呼ぶ。
次に前章と同様に考えて(1)にエネルギー積分をすると、
\[\dot{K_i}=\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}\cdot\boldsymbol{v}_{i}+\boldsymbol{F}^{(ex)}_{i}\cdot\boldsymbol{v}_{i}\]
$i=1,2,\cdots,N$について足すと、
\begin{eqnarray}
\dot{K}
&=&\dot{K}_{G}+\dot{K}_{in}\\
&=&\displaystyle\sum_{i}\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}\cdot\boldsymbol{v}_{i}+\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i}\cdot\boldsymbol{v}_{i}\\
&=&\displaystyle\sum_{i}\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}\cdot\boldsymbol{v}_{i}\\
&+&\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i}\cdot\boldsymbol{v}_{iG}\\
&+&(\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i})\cdot\boldsymbol{v}_{G}\tag{12}
\end{eqnarray}
ここで、重心運動方程式(5)についてもエネルギー積分すると、
\[M\dot{\boldsymbol{v}}_{G}\cdot\boldsymbol{v}_{G}=(\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_i)\cdot\boldsymbol{v}_{G}\]
$\therefore \dot{K}_{G}=(\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i})\cdot\boldsymbol{v}_{G}\tag{13}$
(12)、(13)より、
$\left\{ \begin{eqnarray}
K
&=&K_G+K_{in}\\
&&\\
\dot{K}_{G}
&=&(\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i})\cdot\boldsymbol{v}_{G}\\
\dot{K}_{in}
&=&\displaystyle\sum_{i}\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}\cdot\boldsymbol{v}_{i}\\
&+&\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i}\cdot\boldsymbol{v}_{iG}
\end{eqnarray} \right.\tag{14}$
この結果より、重心運動には外力のみが影響し、内部運動には外力と内力が影響することが分かる。次に、具体的な状況で考えてみる。
重力
多粒子系に重力が働いている場合、つまり
\[\boldsymbol{F}^{(ex)}_i=m_i\boldsymbol{g}\]
のとき、
\[\displaystyle\sum_{i}\boldsymbol{F}^{(ex)}_{i}\cdot\boldsymbol{v}_{iG}=(\displaystyle\sum_{i}m_{i}\boldsymbol{v}_{iG})\cdot\boldsymbol{g}=0\]
より、外力の内部運動への影響はなく、重心運動への影響のみ考えればよいことがわかる。
$\boldsymbol{F}_{12}$と$\boldsymbol{F}_{21}$の合計の仕事率
二つの質点1,2の間に相互に力が働くとき、二つの力の合計の仕事率は、上で述べた第三法則より、
\[\boldsymbol{F}_{12}\cdot\boldsymbol{v}_{1}+\boldsymbol{F}_{21}\cdot\boldsymbol{v}_{2}=\boldsymbol{F}_{12}\cdot(\boldsymbol{v}_{1}-\boldsymbol{v}_{2})\tag{15}\]
となり、二つの質点の相対運動で考えた内力の仕事率に等しい。これは、何が嬉しいかというと、内力の合計の仕事率を楽に求められるということである。具体的に以下の問題設定で考えてみる。
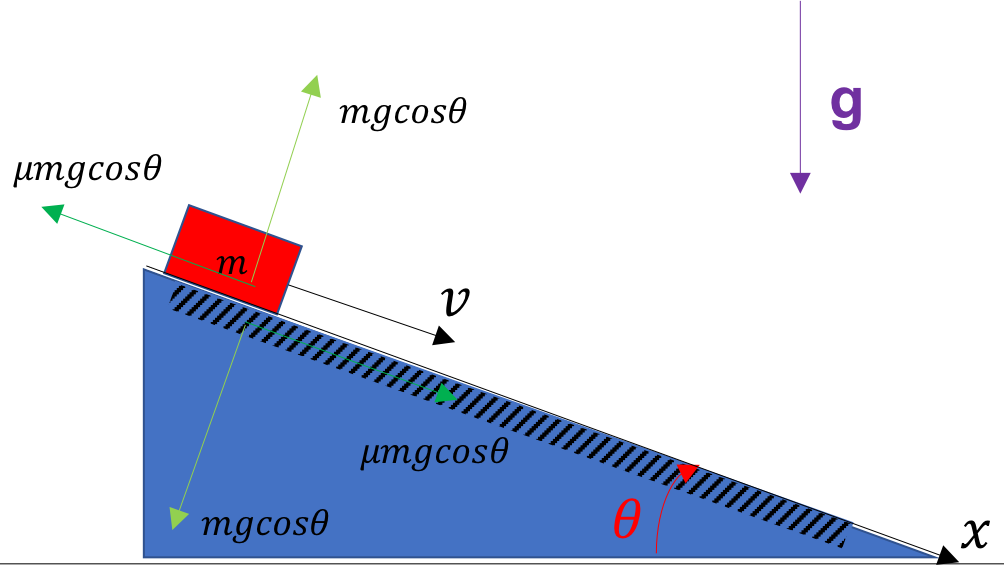
まずは、摩擦力について考える。摩擦力は接触面に平行であるため、(15)と$ \ \boldsymbol{F}_{12}\parallel\boldsymbol{v}_{1}-\boldsymbol{v}_{2} \ $より、
\[(内力である摩擦力の合計の仕事)=-\mu mg\cos\theta\times(物体が滑り降りた距離)\]
となる。
次に、垂直抗力について考える。垂直抗力は接触面に垂直であるため、$ \ \boldsymbol{F}_{12}\perp\boldsymbol{v}_{1}-\boldsymbol{v}_{2} \ $より、
\[(内力である垂直抗力の合計の仕事)=0\]
となる。ここで注意すべきなのは、垂直抗力の合計の仕事が$0$なのであって、それぞれの物体にする仕事は$0$ではないということである。いわゆる垂直抗力が仕事をしないというのは、台が動いてない場合に物体の速度と垂直抗力が垂直となるためで、台が動く場合はその限りではない。垂直抗力というのは、台に対する物体の相対速度と垂直に働くため、この場合、物体の速度(=台に対する物体の相対速度+台の速度)と垂直抗力は垂直とはならないのである。また垂直抗力の合計の仕事が$0$ということはすなわち、垂直抗力が物体にした仕事は、垂直抗力が台にした仕事の逆符号になる。
角運動量
多粒子系の全角運動量$ \boldsymbol{L} \ $について以下が成り立つ。($\because(7), \ (9)$)
\begin{eqnarray}
\boldsymbol{L}
&=&\displaystyle\sum_{i}\boldsymbol{L}_i\\
&=&\displaystyle\sum_{i}\boldsymbol{r}_i\times m_i\boldsymbol{v}_i\\
&=&\displaystyle\sum_{i}(\boldsymbol{r}_G+\boldsymbol{r}_{iG})\times m_i(\boldsymbol{v}_G+\boldsymbol{v}_{iG})\\
&=&\boldsymbol{r}_G\times(\displaystyle\sum_{i}m_i)\boldsymbol{v}_G\\
&+&(\displaystyle\sum_{i}\boldsymbol{r}_{iG}\times m_iv_{iG})\\
&+&\boldsymbol{r}_{G}\times (\displaystyle\sum_{i}m_i\boldsymbol{v}_{iG})\\
&+&(\displaystyle\sum_{i}m_i\boldsymbol{r}_{iG})\times\boldsymbol{v}_G\\
&=&\boldsymbol{r}_G\times M\boldsymbol{v}_G+(\displaystyle\sum_{i}\boldsymbol{r}_{iG}\times m_iv_{iG})\tag{16}
\end{eqnarray}
(16)の第一項を重心角運動量$ \ \boldsymbol{L}_G \ $、第二項を内部角運動量$ \ \boldsymbol{L}_{in} \ $と呼ぶ。
次に前章と同様に考えて$ \ \boldsymbol{r}\times(1) \ $より、
\[\dot{\boldsymbol{L}_i}=\boldsymbol{r}_i\times(\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij})+\boldsymbol{r}_i\times(\boldsymbol{F}^{(ex)}_{i})\]
$i=1,2,\cdots,N$について足すと、
\begin{eqnarray}
\dot{\boldsymbol{L}}
&=&\dot{\boldsymbol{L}}_{G}+\dot{\boldsymbol{L}}_{in}\\
&=&\displaystyle\sum_{i}(\boldsymbol{r}_i\times(\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}))+\displaystyle\sum_{i}(\boldsymbol{r}_i\times(\boldsymbol{F}^{(ex)}_{i}))\\
&=&\displaystyle\sum_{i}(\boldsymbol{r}_i\times(\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}))\\
&+&\displaystyle\sum_{i}(\boldsymbol{r}_{iG}\times(\boldsymbol{F}^{(ex)}_{i}))\\
&+&\boldsymbol{r}_G\times\displaystyle\sum_{i}(\boldsymbol{F}^{(ex)}_{i})\tag{17}
\end{eqnarray}
ここで、重心運動方程式(5)についても$ \ \boldsymbol{r}_{G}\times(5) \ $より、
\[\boldsymbol{r}_G\times M\ddot{\boldsymbol{r}}_G=\boldsymbol{r}_G\times\displaystyle\sum_{i}(\boldsymbol{F}^{(ex)}_{i})\]
$\therefore \dot{\boldsymbol{L}}_G=\boldsymbol{r}_G\times\displaystyle\sum_{i}(\boldsymbol{F}^{(ex)}_{i})\tag{18}$
(17)、(18)より、
$\left\{ \begin{eqnarray}
\boldsymbol{L}
&=&\boldsymbol{L}_G+\boldsymbol{L}_{in}\\
&&\\
\dot{\boldsymbol{L}}_G
&=&\boldsymbol{r}_G\times\displaystyle\sum_{i}(\boldsymbol{F}^{(ex)}_{i})\\
\dot{\boldsymbol{L}}_{in}
&=&\displaystyle\sum_{i}(\boldsymbol{r}_i\times(\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}))\\
&+&\displaystyle\sum_{i}(\boldsymbol{r}_{iG}\times(\boldsymbol{F}^{(ex)}_{i}))
\end{eqnarray} \right.\tag{19}$
ただ、通常そうであるように、内力が中心力である、すなわち、質点同士の相互作用が2粒子を結ぶ直線に沿って働けば($F_{ij}\parallel F_{ji}\parallel (\boldsymbol{r}_i-\boldsymbol{r}_j)$)、作用反作用の法則よりそれぞれの質点に働く内力が相殺して、
\[\boldsymbol{r}_i\times\boldsymbol{F}^{in}_{ij}+\boldsymbol{r}_j\times\boldsymbol{F}^{in}_{ji}=\boldsymbol{0}\]
\[ \therefore (内力のモーメント)=\displaystyle\sum_{i}(\boldsymbol{r}_i\times(\displaystyle\sum_{j}\boldsymbol{F}^{(in)}_{ij}))=\boldsymbol{0}\]
すなわち、この場合の多粒子系の全角運動量の時間変化は、外力のモーメントと等しくなる。次に、具体的な状況で考えてみる。
重力
多粒子系に重力が働いている場合、つまり
\[\boldsymbol{F}^{(ex)}_i=m_i\boldsymbol{g}\]
のとき、
\[\displaystyle\sum_{i}\boldsymbol{r}_{iG}\times\boldsymbol{F}^{(ex)}_{i}=(\displaystyle\sum_{i}m_{i}\boldsymbol{r}_{iG})\times\boldsymbol{g}=\boldsymbol{0}\]
より、外力の内部運動への影響はなく、重心運動への影響のみ考えればよいことがわかる。
